
|
Функция Эйлера 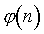 от натурального n есть количество чисел, меньших n
и взаимно простых с n (число 1 взаимно просто с любым числом).
При этом считается, что
от натурального n есть количество чисел, меньших n
и взаимно простых с n (число 1 взаимно просто с любым числом).
При этом считается, что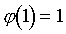 . .
Если мы попробуем
просто проверять все числа, меньшие n, на взаимную простоту
с n, то при больших n программа будет работать часами,
а то и сутками.
Попробуем посмотреть на задачу внимательнее.
Первое, что мы заметим - это
то, что простое число всегда взаимно просто со всеми числами,
меньше себя, значит, для простых n,
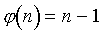 | (1) |
Уже легче. Далее можно
рассмотреть случай, когда n имеет единственный простой
делитель p, повторенный несколько раз, т.е. n=pk
(случай, рассмотренный выше, есть частный случай данного, при
k=1). Очевидно, что такое число будет взаимно просто со
всеми числами, меньше себя, кроме чисел, кратных p. Всего
таких чисел pk-pk-1.
Таким образом, мы можем обобщить выражение (1) для простых p:
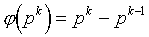 | (2) |
Заметим еще, что, если
некоторые p и q взаимно просты, то число pq
будет взаимно просто со всеми числами, меньшими себя, кроме тех,
которые кратны хотя бы одному делителю p или хотя бы одному
делителю q. Отсюда имеем еще одно свойство функции Эйлера,
а именно: для взаимно простых p и q:
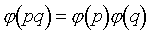 | (3) |
Предположим, что мы разложили
n на простые множители и записали в каноническом виде:
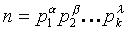 , где все pi различные
простые числа. Тогда, применив (2) и (3), получаем, что , где все pi различные
простые числа. Тогда, применив (2) и (3), получаем, что
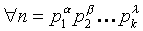 , где p простые, , где p простые,
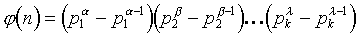 | (4) |
Теперь, наконец, мы можем
предложить приемлемый алгоритм.
Число n следует
разложить на простые множители p1, p2,
..., pk, и представить в каноническом виде.
Затем нужно посчитать выражение (4) и выдать его в качестве результата.
Вот, собственно, и все.
Программа получается очень простая. Все, что нужно, - то
лишь представить n в каноническом виде.
Про разложение числа на множители можно прочитать здесь.
|