По книге "Вычислительная геометрия"
Препарата, Шаймос.

Будем разбивать исходное множество на части, находить их выпуклые оболочки, а потом сливать их в одну общую.

Предположим, при решении задачи построения выпуклой оболочки, исходное множество точек было разбито на две части S₁ и S₂, каждая из которых содержит половину точек исходного множества. Если теперь рекурсивным образом найдены отдельно CH(S₁) и CH(S₂), то каковы дополнительные затраты, необходимые для построения CH(S₁ U S₂), т.е. выпуклой оболочки исходного множества? Для ответа на этот вопрос можно воспользоваться следующим соотношением:

	CH(S1 U S2) = CH(CH(S1) U CH(S2))     (1)
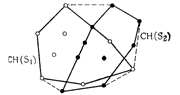
Рис. 1: Разбив множество S на два подмножества и построив рекурсивно выпуклые оболочки этих подмножеств, можно свести исходную задачу к построению выпуклой оболочки объединения двух выпуклых многоугольников

Хотя при первом взгляде на соотношение (1) кажется, что такой способ требует больших затрат, чем прямой способ построения выпуклой оболочки, решающее соображение состоит в том, что CH(S₁) и CH(S₂) -это не просто неупорядоченные множества точек, а выпуклые многоугольники (рис. 1).

Помимо того что эта задача интересна сама по себе, онат важна и в силу того, что представляет собой шаг слияния процедуры "разделяй и властвуй" и, таким образом, дает фундаментальное средство для решения геометрических задач. Нельзя; надеяться, что окончательный алгоритм будет эффективным, до тех пор, пока решения подзадач не могут быть быстро объединены.

procedure ОБОЛОЧКА (S)
1. Если |S| < k0 (k0 - некоторое небольшое целое число),
   то построить выпуклую оболочку одним из прямых методов и остановиться;
   иначе перейти к шагу 2.

2. Разбить исходное множество S произвольным образом
   на два примерно равных по мощности подмножества S1 и S2.
   
3. Рекурсивно найти выпуклые оболочки S1 и S2.
4. Слить (соединить) две получившиеся оболочки вместе, образуя CH(S).

Обозначим символом U(N) время, необходимое для нахождения выпуклой оболочки объединения двух выпуклых многоугольников, каждый из которых имеет N/2 вершин. Если T(N) - время, необходимое для нахождения выпуклой оболочки множества из N точек, то, применяя соотношение (1), получаем

Следующий алгоритм "слияния" предложен М. Шеймосом:

1. Найти некоторую внутреннюю точку р многоугольника Р1 (Например, центроид трех любых вершин Р1. Такая точка р будет внутренней точкой CH(P₁UP₂)).

	CH(S1 U S2) = CH(CH(S1) U CH(S2))     (1)
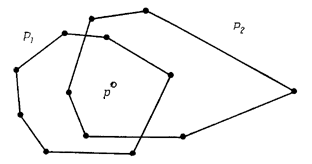
Рис. 2: Точка р находится внутри многоугольника Р2. Так как точка р одновременно находится внутри обоих многоугольников Р1 и Р2, то их вершины упорядочены по значению полярного угла точки р. Слияние двух упорядоченных множеств вершин можно выполнить за линейное время

2. Определить, является ли р внутренней точкой Р2. Это может быть сделано за время O(N). Если р не является внутренней точкой Р2, перейти к шагу 4.

3. р является внутренней точкой Р2 (рис. 2). Тогда вершины как Р1, так и Р2 оказываются упорядоченными в соответствии со значением полярного угла относительно точки р. За время O(N) можно получить упорядоченный список вершин как P1, так и Р2 путем слияния списков вершин этих многоугольников. Перейти к шагу 5.

4. р не является внутренней точкой Р2 (рис 3). Если смотреть из точки р, то многоугольник Р2 лежит в клине с уголом разворота меньшим или равным пи. Этот клин определяется двумя вершинами u и v многоугольника Р2, которые могут быть найдены за линейное время за один обход вершин многоугольника Р2.

	CH(S1 U S2) = CH(CH(S1) U CH(S2))     (1)
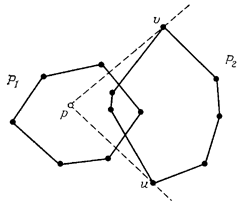
Рис. 3: Точка р находится вне многоугольника P2. Многоугольник Р1 находится внутри угла, определяемого точками v, р, u. Точки v и u разбивают последовательность вершин многоугольника Р2 на две цепи. Одну из них можно удалить, а слияние вершин второй цепи с упорядоченным множеством вершин многоугольника P1 можно выполнить за линейное время

Проходим по вершинам, находя самую правую и самую левую. Операция занимает линейное время, но работает для любых простых многоугольников. Для выпуклых многоугольников, вообще говоря, есть алгоритм, выполняющий поиск u,v за logn операций (через бинарный поиск), но здесь он описываться не будет, так как улучшения в общем все равно будут незначительные.

В примере кода ниже многоугольник хранится кольцевым списком вершин, основная функция, возвращающая u(=ltan) и v(=rtan): tangent_PointPoly().

// Point type
typedef struct coord_ {
  float x;
  float y;
} coord;

// Ring type = polygon
typedef struct ring_ {
  coord data;
  struct ring_ *next;
  struct ring_ *prev;
} Ring;


// isLeft(): tests if a point is Left|On|Right of an infinite line.
//    Input:  three points P0, P1, and P2
//    Return: >0 for P2 left of the line through P0 and P1
//            =0 for P2 on the line
//            <0 for P2 right of the line
inline float
isLeft( coord *p0, coord *p1, coord *p2 ) {
    return (p1->x - p0->x)*(p2->y - p0->y) - (p2->x - p0->x)*(p1->y - p0->y);
}


// tangent_PointPoly(): find any polygon's exterior tangents
//    Input:  p = a 2D point (exterior to the polygon)
//            P = vertices for any 2D polygon
//    Output: rtan = pointer to the rightmost tangent point
//            ltan = pointer of leftmost tangent point
void
tangent_PointPoly( coord *p, Ring *P, Ring **rtan, Ring **ltan ) {
  float  eprev, enext;       
  Ring *cur;
  
  cur = P->next;    
  *rtan = P;  // initially assume *P = both tangents
  *ltan = P;

  eprev = isLeft(&(P->data), &(P->next->data), p);

  do {
    enext = isLeft( &(cur->data), &(cur->next->data), p);
    if ((eprev <= 0) && (enext > 0)) {
      if (isLeft(p, &(cur->data), &((*rtan)->data)) >= 0)
        *rtan = cur;
    }
    else if ((eprev > 0) && (enext <= 0)) {
      if (isLeft(p, &(cur->data), &((*ltan)->data)) <= 0)
        *ltan = cur;
    }
    eprev = enext;
    cur = cur->next;
  } while (cur != P);
  
  return;
}

Эти вершины разбивают границу Р2 на две цепи вершин, являющиеся монотонными относительно изменения полярного угла с началом в р. При движении по одной цепи угол увеличивается, при движении по другой - уменьшается. Одна из этих двух цепей, являющаяся выпуклой по направлению к точке р, может быть немедленно удалена, так как ее вершины будут внутренними точками CH(S₁ U S₂). Другая цепь Р2 и граница P1 представляют два упорядоченных списка, содержащих в сумме не более N вершин. За время О(N) их можно слить в один список вершин P1 U P2, упорядоченных по углу относительно точки р.

5. Теперь к полученному списку можно применить метод обхода Грэхема (шаг 2 алгоритма 'обход Грэхема'), требующий лишь линейное время. Теперь получена выпуклая оболочка Р1 U P2. Если многоугольник P1 имеет m вершин, а Р2 имеет n вершин, то время выполнения этого алгоритма равно O(m+n), что со всей очевидностью является оптимальным. Так что теперь известно, что U(N) = O(N), и решением рекуррентного соотношения (1) в этом случае является T(N) = O(NlogN).