Алгоритм Диница.

 

Этот алгоритм, опубликованный в 1970 г., имел огромное значение. На протяжении 10 лет все достижения в решении задачи о максимальном потоке базировались на методе Диница.

Основная идея метода – алгоритм состоит из фаз, на которых поток увеличивается сразу вдоль всех кратчайших цепей определенной длины.  Для этого на i-той фазе строится вспомогательная бесконтурная сеть (layered network). Эта сеть содержит все увеличивающие цепи, длина которых не превышает k_i, где k_i – длина кратчайшего пути из s в t. Величину  k_i называют длиной вспомогательной сети.

 

Рассмотрим работу алгоритма на i-той фазе:

 

Шаг 1. Построение вспомогательной сети.

С помощью поиска в ширину мы движемся из источника сети в сток по допустимым дугам, добавляя их в S_k и увеличивая k. Дуга u добавляется с c_k(u) = c(u) – f(u). Как только достигнут сток сети, он помечается величиной k и k становится “фиксированной”. Мы продолжаем поиск в ширину, но он уже не ведется из вершин v, для которых q(s, v) ≥ k. Таким образом, вспомогательная сеть будет содержать подсеть исходной. Если поиск в ширину не достиг стока, то работа алгоритма прекращается. Если k больше (k может только увеличиваться) k_i, то мы находимся на i+1 фазе с k_i+1 = k.

Шаг 2. Поиск псевдомаксимального потока.

В построенной нами бесконтурной сети длины k ищется псевдомаксимальный поток. Под псевдомаксимальным потоком понимается такой поток f, для которого не существует увеличивающих цепей длины k. Найденный поток переносится в исходную сеть. Затем мы вновь переходим к первому шагу.

Для построения псевдомаксимального потока используется поиск в ширину (с ограничением на длину пути). Пусть на j-той итерации был найден путь из s в t. Пустим по этому пути поток f_j. Это значит, что как минимум одна дуга вспомогательной сети является насыщенной. Удалим все насыщенные дуги. В результате могут образоваться “тупики”: вершины, из которых не выходит ни одна дуга (кроме стока), вершины, в которые не входит ни одна дуга (кроме источника) и изолированные вершины. Их также следует удалить со всеми инцидентными им дугами. Это в свою очередь может привести к образованию новых тупиков. Корректировка производится, пока во вспомогательной сети не останется ни одного тупика. Изменим пропускные способности оставшихся дуг по формуле c_k(u) = c_k(u) – f_j(u).

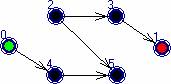
рис. 4

На рисунке вершины 2 и 5 являются тупиками. После их удаления будут последовательно удалены все вершины сети.

 

Поиск f_j следует продолжать до тех пор, пока вспомогательная сеть ≠ Ø. Очевидно, что псевдомаксимальный поток f = ∑ f_j. Псевдомаксимальный поток можно хранить в какой-либо структуре, но на практике найденные потоки f_j обычно сразу переносятся в исходную сеть S.

Заметим, что после нахождения fi и корректировки сети, поиск в ширину можно продолжать с ближайшей к s не подвергшейся изменениям дуги найденного пути.

 

После завершения работы Алгоритма исходная сеть будет содержать максимальный поток. Пример:

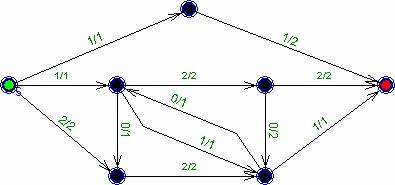
рис. 5.

 Сеть с уже найденным с помощью алгоритма Диница максимальным потоком.

 

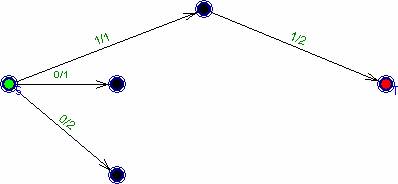
рис. 6.

Вспомогательная сеть на 1 фазе. k₁ = 2.

 

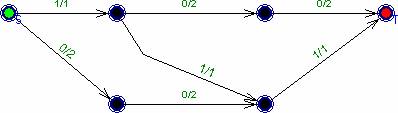
рис.7.

Вспомогательная сеть на 2 фазе. k₂ = 3. На этой сети хорошо видно, что псевдомаксимальный поток обычно не является максимальным.

 

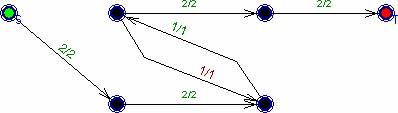
рис.8.

Вспомогательная сеть на 3 фазе. k₃ = 5.

 

 

Метод поразрядного сокращения невязок.

 

В зарубежной литературе этот метод получил название capacity scaling. Он был рассмотрен Эдмондсом и Карпом в 1972 и независимо Диницом в 1973. Если с его помощью модифицировать алгоритм кратчайших увеличивающих цепей или алгоритм Диница, то можно получить оценки быстродействия O(m² Log U) и O(mn Log U) соответственно, где U = max(C_ij).

Возьмем достаточно большое целое K (т.н. масштаб). Пусть все пропускные способности дуг округлены с недостатком до ближайшего кратного числу K и формируют сеть CS_k. Тогда при увеличении потока в этой сети, он будет возрастать на целое, кратное K. Таким образом, для построения потока мощности M требуется не более M/K итераций. Как только в сети CS_k найден максимальный поток, уточним пропускные способности дуг, выбрав K’ и округлив их с недостатком до ближайшего кратного числу K’. Где K’ < K. После корректировки сети CS_k и потока f(u), получим сеть CS_k’ с потоком f’(u). Если K кратно K’, то имеющийся поток останется целочисленным. Полученный на предыдущей итерации поток следует увеличить, чтобы он вновь стал максимальным. Подбирая, таким образом, масштаб, мы все более полно будем использовать пропускные способности дуг. В случае целочисленных пропускных способностей, максимальный поток будет получен после его увеличения в масштабе K = 1.

На практике выбирают K = log₂U. На i-той итерации берется масштаб 2^(K-i+1). В целочисленном случае для нахождения максимального потока достаточно K+1 итерации.