Алгоритм Галила-Наамада (Galil and Naamad).

 

 Предложен в 1980г и имеет оценку O(nm*log²(N)). Данный алгоритм был также независимо рассмотрен Shiloach

 Метод базируется на алгоритме Диница и в его основе лежит усовершенствование метода построения псевдомаксимального потока. Рассмотрим путь из s в t, найденный в Sk на i-той итерации:

 

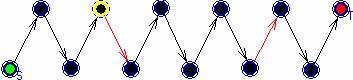
рис. 9.

 

Пусть после увеличения потока в этой цепи, помеченные на рисунке дуги стали насыщенными (а как минимум одна насыщенная дуга в цепи появится). После корректировки сети эти дуги удаляются, и поиск пути из s в t продолжится из вершины, окрашенной желтым. Информация об остальных участках цепи будет утрачена, эти части могут быть заново пройдены - что не эффективно. Подобные участки Галил и Наамад назвали “Фрагментами пути”. Сохраняя информацию об этих фрагментах и используя ее для построения цепи из s в t, им удалось увеличить быстродействие алгоритма Диница.

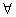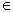 Рассмотрим операции, определенные для фрагментов пути. Пусть PF1 и PF2 – два фрагмента пути. Обозначим s(PF) – начальную вершину пути PF, e(PF) – конечная вершина PF, v(PF) – множество внутренних вершин PF (v  PF \ {s(PF), e(PF)}). Если e(PF1) = s(PF2), для фрагментов допустима операция объединения. Результатом будет являться PF = PF1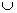PF2. В случае, когда e(PF1) = w 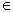 v(PF2), PF2 может быть разделен на 2 фрагмента PF3 и PF4, где e(PF3) = w и s(PF4) = w. Затем PF1 и PF4 можно объединить. 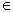Для любой вершины сети v, может существовать только один фрагмент пути, для которого vv(PF), либо v = s(PF). Но могут иметься несколько фрагментов, оканчивающихся на эту вершину.

Для хранения информации о фрагментах пути и проведения операций над ними, используются специальные структуры – “2-3 деревья”. В рамках этой работы мы не будем их рассматривать. Разработка эффективных способов представления деревьев и сетей является отдельным направлением исследований. Использованные в алгоритме 2-3 деревья подробно описаны в [8].

Спустя некоторое время, совместно Слейтор и Тарян (Sleator and TarJan) предложили структуру данных, обеспечивающую еще большее быстродействие [9]. С помощью этой структуры оценка алгоритма Галила-Наамада может быть улучшена до O(nm log n).