Алгоритм Карзанова.

 

Карзанову в 1974г удалось, с помощью модификации алгоритма Диница, добиться оценки быстродействия O(n³). Им также впервые было введено понятие “предпотока”. Дадим следующие определения:

 

Путь L_v,t из вершины v в сток t называется блокированным, если он содержит хотя бы одну насыщенную дугу.

Вершина (дуга) блокирована, если блокирован любой проходящей через нее путь.

Поток f в S_k называется тупиковым, если блокирован источник s.

Предпотоком назовем поток g, удовлетворяющий 4-м условиям:

 

1.      0 ≤ g(u) ≤ c_k(u), где u – дуга S_k сети, c_k(u) – ее пропускная способность.

2.      Для любой вершины v 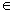 V_k \ {s, t}, div (v) ≤ 0.

3.      если div (v) < 0, то v – g-блокирована.

4.      источник s g-блокирован.

 

Согласно теореме, доказательство которой приведено в [7], если на i-ом этапе увеличить поток сети с помощью тупикового потока вспомогательной сети, то все кратчайшие увеличивающие пути длины k_i будут исчерпаны, и алгоритм перейдет на следующий этап. Это значит, что последовательное построение псевдомаксимальных потоков в S_k сети, может быть заменено поиском тупикового потока. Далее рассматривается алгоритм построения тупикового потока в S_k сети.

 

Для работы необходимы следующие структуры данных:

A(v) – список исходящих из вершины v дуг. Строится для каждой вершины => n списков.

Q(v) – список “добавок” предпотока на дугах, входящих в вершину v. Добавка должна содержать информацию о величине добавки (q(u) > 0) и адрес (либо любой другой идентификатор) дуги u. Необходимо n таких списков. Список Q может содержать несколько добавок, относящихся к одной и той же дуге u.

g(u) – список из m элементов (одномерный массив), содержит текущие значения потока g на дугах u. Отметим, что g(u) = ∑ q(u) из Q(v), где v – конец дуги u.

Dv(v) - список из n элементов (одномерный массив), содержит div (v) для всех вершин v.

D – список дефицитных вершин.

 

Инициализация.

Дана S_k сеть. На всех дугах u исходящих из источника s увеличим поток g на величины, равные пропускным способностям этих дуг (изменяем g(u)). Для всех v смежных с s Dv(v) = - c_k(s, v), а в Q(v) заносится добавка q(u) = c_k(u). Для остальных вершин Dv(v) = 0, списки Q(v) – пустые. D – пуст. Поток g на данный момент не является предпотоком, т.к. не удовлетворяет 3-му условию. Далее производится процедура “Достройки” (будет рассмотрена позднее), которая превратит g в предпоток и заполнит список D.

 

Нахождение тупикового потока S_k сети – итеративный процесс. На каждой итерации выполняются 2 процедуры: “балансирование” и “достройка”. Достройка производится только в случае необходимости, балансирование – всегда. Тупиковый поток будет построен, как только список дефицитных вершин D станет пустым.

 

Балансирование.

Перед началом балансирования g – всегда предпоток. Балансирование производится на дефицитных вершинах D максимального ранга (максимально удаленных от источника s). Заметим, что по построению, вершины в списке D упорядочены по возрастанию рангов (за исключением случая, который будет оговорен позднее), поэтому, чтобы перебрать все дефицитные вершины максимального ранга, нужно просматривать элементы с конца списка D, до тех пор, пока ранг не изменится.

Балансирование вершины v заключается в получении div(v) = 0, с помощью изменения величины g на входящих в v дугах. Для этого берется элемент q(u) из Q(v), его значение необходимо уменьшить на y = min{q(u), -div(v)}. Если после уменьшения div(v) все еще < 0, то q(u) = 0. Удаляем q(u) (в [7] доказано, что можно и не удалять) из Q(v) и берем следующий элемент Q(v). Как только div(v) = 0, балансировка в вершине v прекращается (вершина v удаляется из D) и начинается балансировка следующей вершины. При изменении уменьшении q(u) также должны производится следующие изменения: g(u) := g(u) – y, Dv(v) := Dv(v) + y, Dv(v’) := Dv(v’) – y, где v’ – вершина, из которой исходит дуга u. До уменьшения q(u), Dv(v’) ≤ 0. Если Dv(v’) было < 0, то v’ уже есть в списке D и никаких дополнительных действий предпринимать не следует. Если Dv(v’) было = 0, то теперь вершина v’ “разбалансирована”. Подобные вершины называются источниковыми и дописываются в конец D. Это нарушает порядок следования вершин в D, но, т.к. все источниковые вершины имеют ранг на 1 меньший, чем вершины, подвергнувшиеся балансировке, а они в свою очередь, после балансировки будут удалены из D, то элементы в D вновь станут упорядоченными по возрастанию рангов. При реализации метода, необходимо следить, чтобы балансировка продолжалась с вершины, которая была последней в D до начала балансировки, а не с добавляемых к D источниковых вершин. Также удобно ввести переменную, хранящую адрес 1-й источниковой вершины в D.

 

Достройка.

Достройка необходима в том случае, если g не является предпотоком или в D содержатся  источниковые вершины. Достройка производится последовательно в каждой вершине списка D, начиная с первой источниковой вершины до конца списка. Во время выполнения достройки в вершине, могут быть получены новые дефицитные вершины – они также дописываются в конец D и участвуют в достройке. Т.о. процедура достройки обрабатывает все источниковые и новые дефицитные вершины. При помещении в список новых дефицитных вершин, упорядоченность элементов по возрастанию рангов сохраняется.

Достройка в вершине. Пусть v – обрабатываемая вершина. Цель достройки – получение div(v) = 0, либо сделать ее блокированной. Для этого изменениются величины g(u) для u 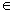 A(v). Последовательно обрабатываем дуги u из A(v). Пусть u = (v, v’). Если A(v’) пуст, то вершина v’ блокирована => дуга u блокирована. В этом случае достройка в u не производится и u удаляется из A(v). Если же A(v’) не пуст, то не известно, блокирована дуга u или нет. Увеличим g(u) на y = min{c_k(u) – g(u), -div(v)}. Внесем изменения и в остальные структуры: Dv(v) := Dv(v) + y, Dv(v’) := Dv(v’) – y. Добавим q(u) = y в список Q(v’). Если div(v) до изменения была = 0, то теперь она стала новой дефицитной вершиной и должна быть занесена в D, если div(v) была < 0, то она уже содержится в D.

Если после увеличения g(u) div(v) < 0, то g(u) = c_k(u) – дуга u становится g-блокированной, удаляется из A(v) и процедура обрабатывает следующую дугу из списка. Если же div(v) = 0, то в вершине v установлен баланс – вершина удаляется из D, достройка в этой вершине прекращается.

Т.к.  при достройке предпотока в D заносятся только вершины, ранее ему не принадлежавшие, то рост списка D конечен.