Алгоритм Кинга.

 

Работа Кинга, Рао и Таряна (King, Rao & Tarjan) опубликована в 1992г. В 1990г. Алон (Alon) предложил свой вариант алгоритма CHM, выработав постоянную стратегию алгоритма-игрока, и добился быстродействия O(mn + n ^8/3Log n). Кинг выдвинул еще более успешную адаптивную стратегию для алгоритма-игрока, улучшив эту оценку до O(nm + n^2+e), что давало O(mn) для всех m > n^1+e. Это позволило увеличить диапазон m/n, для которого на тот момент можно было достичь быстродействия O(nm).

Кинг немного модифицировал правила игры.

Рассмотрим неориентированный двудольный граф G = (U, V, E). |U| = |V| = n, |E| = m. Во время инициализации, алгоритм-игрок назначает дугу каждой вершине из U. Затем игра продолжается по раундам, пока все вершины из V не будут удалены.

Соперник может сделать один из следующих ходов:

1. Удалить любую дугу из графа (edge-kill), но не получит за это очков.

2. Удалить любую вершину из V вместе с инцидентными ей дугами, получив по одному очку за каждую дугу.

Алгоритм-игрок может сделать любую последовательность следующих ходов:

1. Назначить дугу каждой вершине u из U, для которой еще не назначена дуга.

2. Назначить вершине новую инцидентную дугу. Старая дуга приобретает обычный статус, а соперник получает дополнительное очко.

 

Стратегия алгоритма-игрока:

Пусть l – минимальный коэффициент (k) вершин u. Выделим множество U’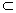U вершин, с коэффициентом больше k. Всех v из V сопоставим оценку r(v), равную числу назначенных дуг (u, v), инцидентных v с минимальным коэффициентом. Диапазон значений, которые могут принимать оценки, можно разделить на уровни. Уровень i содержит вершины, оценки которых лежат в интервале [r_i, r_i+1), где r_i = 2ⁱr₀. Поэтому, вершине из U’ достаточно “знать” уровни смежных вершин. 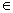Когда для вершины u  U’ назначается дуга, алгоритм выбирает дугу инцидентную вершине с минимальным уровнем.

Подобная стратегия приводит к алгоритму с оценкой O(nm + n^2+e).