Основные определения и теоремы.

 

В этой главе приведены определения и теоремы без доказательства из [1] и [2].

Рассмотрим орграф G = (V, E), где V – множество вершин, E – множество ребер. |V| = n, |E| = m. Под сетью понимается пара S = (G, c), где c: ER – функция, ставящая каждой дуге в соответствие положительное вещественное число – пропускную способность.

Вы делим в сети 2 вершины: s (источник) и t (сток).

Назовем функцию f: ER потоком в сети S, если она удовлетворяет следующим условиям:

1.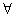(v, u)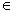E, 0 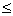 f(v, u)  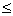c(v, u) – ограничение, накладываемое пропускной способностью дуги.

2.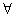v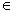V \ {s, t}, 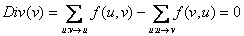- закон сохранения потока[1]

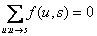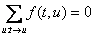, . Величиной потока f, назовем Div(s).

Под максимальным потоком сети понимается поток из s в t максимальной величины.

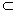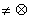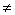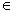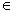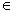Разрезом P(W) сети S, где WV (W, WV), назовем множество дуг (u, v)E, таких, что u V и vV\W.

Поток через разрез определяется так: f(W, V\W) .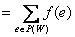

Под пропускной способностью разреза понимается.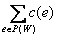

Минимальным разрезом сети называется произвольный разрез P(W), s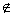W и t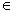V\W с минимальной пропускной способностью.

 

Дадим следующие теоремы без доказательства:

1.      Если s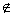W и t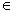V\W, то величина потока из s в t равна f(W, V\W) – f(V\W, A).

2.      Величина каждого потока из s в t не превосходит пропускной способности минимального разреза, разделяющего s и t, причем существует поток, достигающий этого значения. (Теорема Форда-Фалкерсона).

 

Допустимой дугой e = (u, v) относительно потока f назовем дугу, для которой выполняется одно из двух следующих условий:

а). e = (u, v) и f(e) < c(e).

б). e = (v, u) и f(e) > 0.

 

Если для допустимой дуги выполнено первое условие, назовем ее согласованной, иначе не согласованной.

Увеличивающей цепью (длины l) из s в t называется произвольная знакопеременная последовательность (попарно различных) вершин и дуг: v₀, e₁, v₁, e₂, v₂, …, v_l-1, e_l, v_l , где v₀ = s, v_l = t, для всех i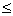l. Все дуги должны быть допустимы.

Зная увеличивающую цепь, мы можем увеличить поток в этой цепи на 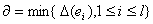, где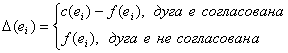

Чтобы увеличить поток, необходимо увеличить его значение на 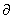 в каждой согласованной дуге цепи и уменьшить в каждой несогласованной.

 

Следующие 3 условия эквивалентны:

1.                        Поток из s в t максимален.

2.                        Не существует увеличивающей цепи для f.

3.                        Величина потока равна c(W, V\W) для некоторого W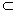V, такого что s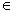W, а t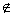W.

 

Теорема о Декомпозиции.

Любой поток из s в t можно разделить на следующие примитивы:

а). Цепь из s в t с потоком величины .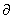

б). Циклы с потоком величины .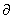

Поток может распасться не более чем на m примитивов.