|
|
Гамма-функция, задаваемая соотношением
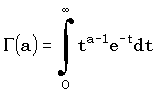 ,
,
входит в нормирующий множитель практически во все функции распределения. Поэтому, естественно, важно уметь ее вычислять. Трудность, однако, в том, что эта функция очень быстро растет: ведь для нее выполнено соотношение  , т.е. для целых аргументов она растет как факториал, и не медленнее для дробных.
, т.е. для целых аргументов она растет как факториал, и не медленнее для дробных.
Быстрый рост чисел, с которыми приходится оперировать, необходимо учитывать и при вычислении собственно функций распределения. Скажем, вычисляя гамма-распределение, мы должны помнить о том, что неполная гамма-функция, нормирующим множителем для которой является 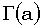 , при большом аргументе становится близкой к
, при большом аргументе становится близкой к 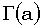 . т.е. тоже большой. Поэтому, не удается разделить вычисления – сначала вычислить неполную гамма-функцию, потом полную, а потом поделить одну на другую. Приходится изобретать уловки, позволяющие справиться с ситуацией.
. т.е. тоже большой. Поэтому, не удается разделить вычисления – сначала вычислить неполную гамма-функцию, потом полную, а потом поделить одну на другую. Приходится изобретать уловки, позволяющие справиться с ситуацией.
Стандартная «волшба» в подобных случаях – разделить вычисляемую функцию на произведение «трудной» и легкой частей, где «трудная» часть является произведением двух или большего числа быстро растущих сомножителей, и вычислять не саму «трудную» часть, а логарифм от нее.
Вот и пример.
При x < a+1 для вычисления функции гамма-распределения  мы используем разложение
мы используем разложение
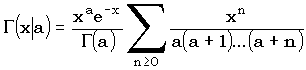 ,
,
распадающееся на «простую» часть 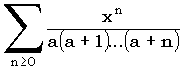 , при работе с которой мы не сталкиваемся с слишком большими числами (факториал в знаменателе растет быстрее степени), и «трудную», которую мы вычисляем как
, при работе с которой мы не сталкиваемся с слишком большими числами (факториал в знаменателе растет быстрее степени), и «трудную», которую мы вычисляем как 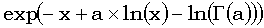 . При x > a+1, для вычисления гамма-распределения используется разложение в цепную дробь, куда входит аналогичный «трудный» сомножитель.
. При x > a+1, для вычисления гамма-распределения используется разложение в цепную дробь, куда входит аналогичный «трудный» сомножитель.
Другой пример. Вычисляя бета-распределение 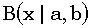 при небольших x, мы используем цепную дробь
при небольших x, мы используем цепную дробь
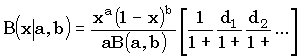 .
.
И снова разложение распадается, и «трудную» часть мы вычисляем как 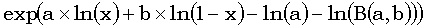 . И снова нужно уметь вычислять логарифм гамма-функции, поскольку
. И снова нужно уметь вычислять логарифм гамма-функции, поскольку 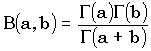 .
.
В нижеследующих кодах используется асимптотическое разложение логарифма гамма-функции, которое (к сожалению, в недостаточно полном виде) можно найти в горячо рекомендуемом справочнике по специальным функциям М.Абрамовица и И.Стигана:
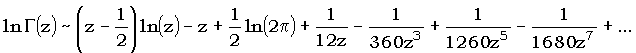
Когда аргумент z достаточно велик, его первые 20 членов дают около 50 верных знаков, если не учитывать ошибки, вызываемые конечной разрядностью. Отражением асимптотического характера ряда в кодах является увеличение слишком малого аргумента: если z меньше некоей границы (в данных кодах 7), он увеличивается, причем для корректировки используется упомянутое выше соотношение  .
.
#ifndef __LOGGAMMA_H__ /* To prevent redefinition */ #define ENTRY extern #define LOCAL static ENTRY double logGamma(double x); /* * Вычисляет натуральный логарифм полной гамма-функции Gamma(x) */ #define __LOGGAMMA_H__ /* Prevents redefinition */ #endif /* Ends #ifndef__LOGGAMMA_H__ */ |
#include <math.h>
#include <assert.h>
#include "logGamma.h"
/***********************************************************/
/* logGamma */
/***********************************************************/
#define LGM_LIM 7
/* Implementation dependent const used to increase
* convergence in logGamma and gammaDF.
* May be changed when porting functions to
* computers with different float/double lengths.
*/
ENTRY double
logGamma(double x)
/*
* Compute natural logarithm of Gamma(x)
* using the asymptotic Sterling's expansion.
* See Abramowitz & Stegun,
* Handbook of Mathematical Functions, 1964 [6.1.41]
* The first 20 terms give the result with 50 digits.
* If x <= 0, assert() is called to indicate error.
*/
{
long double static c[20] =
{
/* Asymtotic expansion coefficients */
1.0 / 12.0, -1.0 / 360.0, 1.0 / 1260.0, -1.0 / 1680.0, 1.0 / 1188.0,
-691.0 / 360360.0, 1.0 / 156.0, -3617.0 / 122400.0, 43867.0 / 244188.0,
-174611.0 / 125400.0, 77683.0 / 5796.0, -236364091.0 / 1506960.0,
657931.0 / 300.0, -3392780147.0 / 93960.0, 1723168255201.0 / 2492028.0,
-7709321041217.0 / 505920.0, 151628697551.0 / 396.0,
-26315271553053477373.0 / 2418179400.0, 154210205991661.0 / 444.0,
- 261082718496449122051.0 / 21106800.0
};
double x2, presum, sum, den, z;
int i;
assert(x > 0); /* Negative argument: Error! */
if (x == 1 || x == 2)
return 0;
for (z = 0; x < LGM_LIM; x += 1) /* Increase argument if necessary. */
z += log(x);
den = x;
x2 = x * x; /* Compute the asymptotic expansion */
presum = (x - 0.5) * log(x) - x + 0.9189385332046727417803297364;
for (i = 0; i < 20; i++) {
sum = presum + c[i] / den;
if (sum == presum) break;
den = den * x2;
presum = sum;
}
return sum - z; /* Fit the increased argument if any */
}/*logGamma*/
|
Дата последней модификации: 25 октября 2000 г.