| Обозначение |
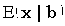
|
| Область значений |
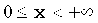
|
| Параметр масштаба | b |
| Плотность (функция вероятности) |
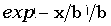
|
| Математическое ожидание | b |
| Дисперсия | b2 |
| Функция распределения |
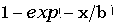
|
Экспоненциальное распределение 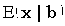 есть частный случай гамма-распределения P(x|a,b) с b=1.
есть частный случай гамма-распределения P(x|a,b) с b=1.
Соответственно, экспоненциальное распределение есть частный случай и распределения Вейбулла W(x|b,c), соответствующий значению параметра c=1.
Экспоненциальное распределение 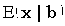 связано с равномерным распределением R на [0,1] следующим соотношением:
связано с равномерным распределением R на [0,1] следующим соотношением: 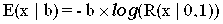 .
.
Сумма n независимых экспоненциально распределенных с параметром b случайных величин 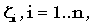 подчиняется распределению Эрланга с параметрами b, n.
подчиняется распределению Эрланга с параметрами b, n.
Случайные числа, соответствующие экспоненциальной случайной величине 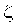 , можно получить из равномерной на [0,1] случайной величины r с помощью соотношения
, можно получить из равномерной на [0,1] случайной величины r с помощью соотношения 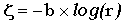 .
.
Не представляет никаких трудностей: используются лишь функции, входящие в стандартные библиотеки (как в Си), либо в сам язык (как в Паскале).
Дата последней модификации: 25 октября 2000 г.