

 |
| Обозначение |
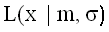
|
| Область значений |
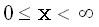
|
| Параметры |
Параметр масштаба (медиана) m > 0, параметр формы (дисперсия) 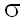 > 0. > 0.
|
| Плотность |
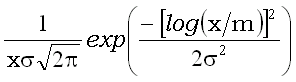
|
| Математическое ожидание |
Не выражается через m и 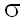 просто. просто.
|
| Дисперсия |
Не выражается через m и 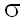 просто просто
|
| Функция распределения | Не выражается в элементарных функциях |
В соответствии с названием, если 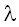 ~
~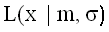 , то случайная величина
, то случайная величина 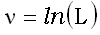 , распределена нормально с параметрами
, распределена нормально с параметрами 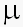 =ln(m) и
=ln(m) и 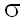 . Таким образом,
. Таким образом, 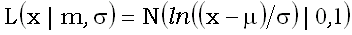 , где
, где 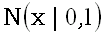 – стандартное нормальное распределение.
– стандартное нормальное распределение.
Указанная связь логнормального распределения 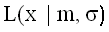 с нормальным
с нормальным 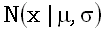 позволяет нам получать случайные числа следующим способом: если r – (стандартное) нормальное случайное число, то
позволяет нам получать случайные числа следующим способом: если r – (стандартное) нормальное случайное число, то 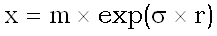 – нужное нам логнормальное случайное число.
– нужное нам логнормальное случайное число.
Из известной связи между стандартным нормальным 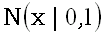 и равномерным R(0,1) распределениями получаем следующую приближенную формулу: если r1, r2,…, r6 – равномерные на отрезке [0,1] случайные величины, то
и равномерным R(0,1) распределениями получаем следующую приближенную формулу: если r1, r2,…, r6 – равномерные на отрезке [0,1] случайные величины, то
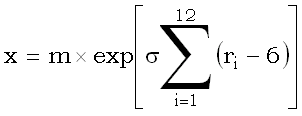
подчиняется приближенно логнормальному распределению: x ~ 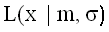 . Таким образом, чтобы получить одно логнормальное случайное число, нужно сгенерировать 6 равномерных, а далее следовать в соответствии с приведенной формулой – вычесть из каждого 6, просуммировать полученные разности и т.д.
. Таким образом, чтобы получить одно логнормальное случайное число, нужно сгенерировать 6 равномерных, а далее следовать в соответствии с приведенной формулой – вычесть из каждого 6, просуммировать полученные разности и т.д.
Связь логнормального распределения 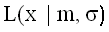 с нормальным
с нормальным 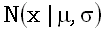 позволяет нам также вычислять значения логнормальной функции распределения и ее квантилей по соответствующим значениям нормального распределения. Действительно, если мы знаем значение стандартного нормального распределения
позволяет нам также вычислять значения логнормальной функции распределения и ее квантилей по соответствующим значениям нормального распределения. Действительно, если мы знаем значение стандартного нормального распределения 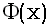 , то
, то 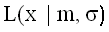 =
=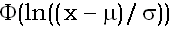 . Таким образом, нам достаточно уметь вычислять стандартное нормальное распределение
. Таким образом, нам достаточно уметь вычислять стандартное нормальное распределение 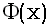 , чего, конечно, и следовало ожидать, исходя из названия.
, чего, конечно, и следовало ожидать, исходя из названия.
Дата последней модификации: 25 октября 2000 г.