| Обозначение |
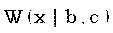 |
| Область значений |
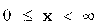 |
| Параметры | Параметр масштаба b > 0 и формы c > 0. |
|
Плотность |
|
|
Математическое ожидание |
|
|
Дисперсия |
|
|
Функция распределения |
|
Распределение Вейбулла 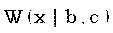 с параметром c = 1 совпадает с экспоненциальным распределением
с параметром c = 1 совпадает с экспоненциальным распределением 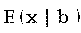 . То же самое формулой:
. То же самое формулой: 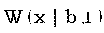 =
= 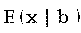 .
.
Распределение Вейбулла 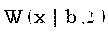 называют еще распределением Релея.
называют еще распределением Релея.
Случайные числа rW для распределения Вейбулла 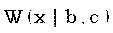 получаются из случайных чисел r для равномерного на [0,1] распределения R согласно формуле
получаются из случайных чисел r для равномерного на [0,1] распределения R согласно формуле 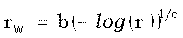 .
.
Не представляет никаких трудностей: используются лишь функции, входящие в стандартные библиотеки (как в Си), либо в сам язык (как в Паскале).
Для совсем ленивых все-таки привожу коды. Помните все же, что использованные стандартные функции работают с ограниченной точностью!
#ifndef __WEIBULL_H__ /* To prevent redefinition */ #define ENTRY extern #define LOCAL static ENTRY double weibullDF(double x, double a, double b); ENTRY double inv_weibullDF(double q, double a, double b); #define __WEIBULL_H__ /* Prevents redefinition */ #endif /* Ends #ifndef__WEIBULL_H__ */ |
#include <assert.h>
#include <math.h>
double weibullDF(double x, double b, double c)
{
assert((b > 0) && (c > 0));
double y = 1-exp(-pow(x/b,c));
return y;
}
double inv_weibullDF(double q, double b, double c)
{
assert((b > 0) && (c > 0) && (q >= 0) && (q < 1));
return q==0 ? 0 : b*pow(-log(1-q),1/c);
}
#ifdef TEST
#include <iostream>
void main(void)
{
double b, c;
while (1) {
cout << "\n\n\rEnter b: ";
cin >> b;
if (b <= 0)
break;
cout << "Enter c: ";
cin >> c;
for(double x=0; x < 8; x += 0.32)
{
double y=weibullDF(x, b, c);
cout << "x=" << x << "\tw=" << y;
double z=inv_weibullDF(y, b, c);
cout << "\tiw=" << z << endl;
}
}
}
#endif |
Дата последней модификации: 25 октября 2000 г.