Задача 1.
Число вводится своим двоичным представлением (длина числа не превышает 10000 двоичных разрядов). Необходимо определить делится ли число на 15.
[Решение]
Задача 2.
Дано число в K-ичной системе счисления
an an-1 ...a0 (K<=36).
Найти остаток от деления его на m.
Числа K, n, m, как и остаток от деления на m, представляются в десятичной системе счисления.
[Решение]
Задача 3.
Любое натуральное число N можно единственным способом представить с помощью некоторых целых неотрицательных d[0], ... , d[s] в виде
N=d[s]*(s+1)!+d[s-1]*s! +...+d[1]*2!+d[0] (*)
при условии, что 0<=d[i]<=i+1, i=0,..,s, где d[s]<>0.
Дано s+1 натуральное число d[0], ..., d[s], и натуральное K, s<200,d[i]<65535, K<65535. Найти остаток от деления числа N, определяемого в факториальной системе (*) числами d[0], ..., d[s], на число K.
[Решение]
Задача 4.
Числа Фибоначчи U[1], U[2], ... определяются начальными значениями U[1]=1, U[2]=2 и соотношением
U[N+1] = U[N] + U[N-1].
Рассмотрим систему счисления с двумя цифрами 0 и 1, в которой, в отличие от двоичной системы весами являются не степени двойки 1,2,4,8,16,..., а числа Фибоначчи 1,2,3,5,8,13,.... В этой системе счисления каждое положительное целое число единственным образом представляется в виде строки нулей и единиц, которая начинается с 1 и в которой нет двух единиц, стоящих рядом.
Даны две строки, представляющие числа A и B. Найти строку, представляющую число A+B.
Пример. Исходные строки '10101' и '100' представляют числа 8+3+1=12 и 3. Ответом является строка '100010', представляющая строку 13+2=15=12+3.
Примечание. Строки могут быть столь длинны, что числа A и B превысят максимально допустимое в вашем компьютере целое число.
[Решение]
Задача 5.
Сосчитать количество единиц в двоичной записи числа i.
[Решение]
Задача 6.
Последовательность 011212201220200112... строится так: сначала пишется 0, затем повторяется следующее действие: уже написанную часть приписывают справа с заменой 0 на 1, 1 на 2, 2 на 0, т.е.
0 -> 01 -> 0112 -> 01121220 ->...
Составить алгоритм, который по введенному N, (0<=N<=3000000000) определяет, какое число стоит на N-ом месте в последовательности.
[Решение]
Задача 7.
Дан массив X(100) и Y(100). Записать алгоритм, меняющий последовательно местами значения элементов X(k) и Y(k) для этих таблиц, для k=1,2,...,100, не используя промежуточных переменных.
[Решение]
Задача 8.
Точки с целочисленными координатами из 1-го квадранта помечаются числами 0,1,2,... слева направо и снизу вверх таким образом, что очередной точке приписывается минимальное число, отсутствующее в вертикали и горизонтали, проходящей через точку. Первой помечается точка (0,0).
Написать программу, которая
1. По заданным координатам x и y, x>=0, y>=0, x,y- целые, определяет пометку точки.
2. По заданной координате x и пометке точки y, x>=0, y>=0, x, y - целые, определяет вторую координату точки.
[Решение]
Задача 10.
Известно, что запись числа A в позиционных системах счисления с основанием p и q имеет вид бесконечной периодической дроби с периодом 2:
A = O,(ab) = O,(ba) (*)
где a и b - различные цифры в этих системах счисления.
Написать программу, которая для введенных натуральных чисел p и q (2<=p,q<=30, p>q) находит и выводит все возможные пары значений цифр a и b, удовлетворяющих соотношению (*). Если таковых нет, вывести сообщение 'Пригодных цифр нет'.
Предусмотреть защиту от ввода ошибочных данных.
Примечание: Значением числа, запись которого в позиционной системе счисления с основанием S есть 0, cdef (где c,d,e,f - цифры), являются
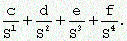
[Решение]
Задача 11.
Определим множества K[i] рекуррентно. Пусть K[0] = [0,1]. Разделим сегмент [0,1] на три части точками 1/3 и 2/3 и удалим из него интервал (1/3,2/3). Получим множество K[1], состоящее из двух оставшихся сегментов [0,1/3] и [2/3,1]. Каждый из них разделим на три части (точками 1/9 и 2/9 для первого сегмента, и точками 7/9 и 8/9 - для второго ) и удалим средние интервалы (1/9,2/9) и (7/9,8/9). Таким образом получаем множество K[2], и т.д. Пусть мы построим множество K[i]. Поделим каждый оставшийся сегмент из K[i] на 3 части и удалим из этих сегментов средние интервалы. Получим, таким образом, из K[i] множество K[i+1].
Вводятся 3 целых числа n,a,b.
Необходимо определить, принадлежит ли точка с координатой a/b множеству K[n].
[Решение]
Задача 12.
Дано натуральное n. Подсчитать количество решений
неравенства x*x + y*y<n в натуральных (неотрицательных целых)
числах, не используя действий с вещественными числами. Количество операций должно быть порядка (n1/2)
[Решение]
Задача 13.
Число называется совершенным, если оно равно сумме всех своих делителей за исключением его самого. Любое четное совершенное число представимо в виде
2p-1 * (2p - 1), где р натуральное число.
Найти двоичное представление для максимального совершенного четного числа меньшего введенного N.
[Решение]
Задача 14.
Заданы натуральные числа E,K,M,T в записи химической реакции
ХеАk + Y -> YmAt + X,
где A,X,Y - атомы или группы атомов. Написать алгоритм, который находит такие натуральные коэффициенты, чтобы знак "стрелки" можно было заменить знаком равенства.
[Решение]
Задача 15.
Вводятся целые числа a и b. Пусть у треугольника ABC координаты A=(0,0), B=(a,b), а обе координаты C=(x,y) - целые числа, и площадь треугольника ABC не равна нулю.
Какую минимальную площадь может иметь треугольник ABC?
[Решение]
Задача 16.
Имеется N банок с целочисленными объемами V1, ..., Vn литров, пустой сосуд и кран с водой. Можно ли с помощью этих банок налить в сосуд ровно V литров воды.
[Решение]
Задача 17.
Функция f с натуральными аргументами
и значениями определена так: f(0)=0, f(1)=1, f(2n)=f(n),
f(2n+1) = f(n) + f(n+1). Составить программу вычисления f (n)
по заданному n, требующую порядка log n операций
[Решение]
Задача 18.
Вывести на экран число 2n, n<=10000, n - натуральное.
[Решение]
Задача 19.
Определить количество повторений каждой из цифр 0,1,2,...,9 в числе NN (N в степени N), N <= 1000.
[Решение]
Задача 21.
Вводится N. Необходимо найти, на сколько нулей оканчивается N!=1*2*3*...*N.
[Решение]
<Задача 22.
На входе программе даются два числа N и P. Программа на выходе должна дать такое максимальное число M, что N! делится на P в степени M, но не делится на P в степени M+1.
Примечание.
1.Числа N и P так велики , что нет смысла считать значение N!.
2.Числа N и P являются натуральными.
[Решение]
Задача 23.
Натуральное число N>1 представить в виде суммы натуральных чисел так, чтобы произведение этих слагаемых было максимально.
[Решение]
Задача 24.
Задается любое положительное действительное число R. Найти положительные действительные R1,R2,...,Rn, Ri<4 ,i=1,...,n, такие, что R=R1*R2*...*Rn=R1+R2+...+Rn
[Решение]
Задача 25.
Даны целые числа А(0),А(1),...,А(5). Найти множество корней уравнения
А(5)*X5 + А(4)*X4 + ... + А(0) = 0,
если известно, что все корни - целые числа, A(0)<>0.
[Решение]
Задача 26.
Вывести в порядке возрастания все обыкновенные несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 15. Массив при этом заводить не следует.
[Решение]
<Задача 27.
Дан многогранник, в вершинах которого записаны целые числа.
Одним ходом можно выбрать одно ребро, и к числу, записанному в одном из его концов прибавить один, а из числа, записанного в другом конце - вычесть 1.
Какому необходимому и достаточному условию должны удовлетворять записанные числа, чтобы с помощью таких ходов можно было добиться, чтобы во всех вершинах был одновременно записан ноль? Ответ обосновать.
[Решение]
Задача 28.
a). Полином
p(x)=A[n]*xn+A[n-1]*xn-1+ ... +A[1]*x+A[0]
задается своими коэффициентами A[n], ... ,A[0]. Найти его значение P в точке x.
b). Число в k-ичной системе задается своим представлением (A[n], ... ,A[0]),т.е. в десятичной системе оно имеет значение
A[n]*kn+A[n-1]*kn-1+ ... +A[1]*k+A[0].
Найти это значение.
[Решение]
Задача 29.
Полином N-ой степени
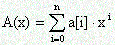
задается своими коэффициентами a[i]. Найти коэффициенты b[i],i=0,...,n*m, m-ой степени полинома A(x). Числа n,m<=40.
[Решение]
Задача 30.
Вычислить коэффициенты A[1], A[2], ..., A[N] многочлена
P(x) =xn + A[1]*xn-1+...+ A[N-1]*x + A[N]
с заданными действительными корнями X[1], X[2], ..., X[N].
[Решение]
Задача 31.
Многочлен
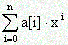
задается набором своих коэффициентов a[i], i=0,..,n. Необходимо вычислить коэффициенты b[i] такого многочлена, что
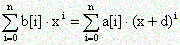
для заданного d.
[Решение]
Задача 32.
Вычислить значение полинома
f(x)=ax4+bx3+cx2+dx+e
для x=1, ..., 10000, используя не более 51000 операций *,+.
[Решение]
|