В процессе отрисовки граней мы почти сразу столкнемся со следующей неприятной ситуацией: проекция грани лежит в плоскости экрана, но она вовсе не обязана точно попадать в прямоугольник-экран. Поэтому эту самую проекцию желательно корректно обрезать по границе экрана (можно, конечно, выводить все на экран через свою функцию putpixel() и проверять в ней x, y на попадание в экран, но это извращение и вдобавок очень медленно). Операцией обрезания как раз и занимаются разные алгоритмы отсечения (clipping).
Это, пожалуй, самый простой, довольно быстрый и наиболее часто используемый метод отсечения. Идея, как обычно, проста. При растеризации треугольника мы в конечном итоге рисуем набор горизонтальных отрезков. Так и будем обрезать по границам экрана именно отрезки. Пусть мы рисуем отрезок от start_x до end_x по строке с y = current_sy. Возможны следующие случаи:
Таким образом, все отсечение делается несколькими строками кода:
// ...
if (current_sy >= YSIZE) return;
if ((current_sy < 0) ||
(start_x >= XSIZE) ||
(end_x <= 0))
break;
if (start_x < 0) {
u -= start_x * du; // пример для аффиного текстурирования
v -= start_x * dv;
}
if (end_x >= XSIZE) end_x = XSIZE - 1;
// ...
Самое приятное заключается в том, что два умножения, которые получаются в случае (start_x < 0), можно легко совместить с теми двумя, что нужны для субтексельной точности (см.п.7.2). А несколько сравнений и присваивание на одну линию делаются достаточно быстро. Получаем отсечение, практически не замедляющее скорость работы.
Этот алгоритм (Sutherland-Hodgman algorithm) предназначен, на самом деле, для отсечения произвольного полигона (даже не обязательно выпуклого, хотя использовать невыпуклые полигоны довольно, на мой взгляд, нерационально) в полуплоскость, или, для 3D случая, в полупространство; другими словами, отсечения полигона прямой или плоскостью. Применяя алгоритм несколько раз, получаем методы отсечения в выпуклый полигон (например, прямоугольник, которым является экран) или выпуклый объем (например, ту часть пространства, которую видно из камеры). Итак, пусть у нас есть полигон с N вершинами, заданными в каком-то порядке, то есть, по часовой стрелке или против; в каком именно, алгоритму все равно. Занумеруем их от 0 до N-1. Теперь последовательно обходим все ребра полигона: ребро от вершины 0 до вершины 1, от 1 до 2, ..., от N-2 до N-1, от N-1 до 0. Вершины, являющиеся началом и концом ребра, могут лежать в области отсечения, (область отсечения - либо полуплоскость для 2D случая, либо полупространство для 3D случая) могут и не лежать; возможны следующие случаи:
Рассмотрим простенький пример работы алгоритма в 2D случае, а именно отсечем 2D треугольник прямой. Она делит плоскость на две полуплоскости, две области, нужную и ненужную. 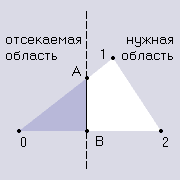
В случае, когда надо сделать отсечение в экран, последовательно применяем алгоритм, отсекая полигон прямыми sx=0, sx=XSIZE, sy=0, sy=YSIZE. Из-за такого простого вида уравнений прямых соответственно упрощается код для выяснения принадлежности вершины нужной области и поиска точки пересечния. Вот, например, кусок кода для отсечения полигона прямой sx=0 (оставляющий область sx > 0).
// dst - массив для сохранения вершин результата
// src - массив вершин исходного полигона
// n - число вершин исходного полигона
// функция возвращает число вершин результата
int clipLeft(vertex *dst, vertex *src, int n) {
int i, r;
vertex p1, p2;
float k;
r = 0;
for (i = 0; i < n; i++) {
p1 = src[i];
p2 = src[(i + 1) % n];
// если начало лежит в области
if (p1.sx >= 0) {
// если конец лежит в области
if (p2.sx >= 0) {
// добавляем начало
dst[r++] = p1;
} else { // если конец не лежит в области
// добавляем начало
dst[r++] = p1;
// добавляем точку пересечения
k = -p1.sx / (p2.sx - p1.sx);
dst[r].sx = 0;
dst[r].sy = p1.sy + k * (p2.sy - p1.sy);
dst[r].u = p1.u + k * (p2.u - p1.u);
dst[r].v = p1.v + k * (p2.v - p1.v);
r++;
}
} else { // если начало не лежит в области
// если конец лежит в области
if (p2.sx >= 0) {
// добавляем точку пересечения
k = -p1.sx / (p2.sx - p1.sx);
dst[r].sx = 0;
dst[r].sy = p1.sy + k * (p2.sy - p1.sy);
dst[r].u = p1.u + k * (p2.u - p1.u);
dst[r].v = p1.v + k * (p2.v - p1.v);
r++;
}
}
}
return r;
}
Видно, что можно чуточку перемешать код обработки разных случаев, изменить порядок действий алгоритма и тем самым подсократить исходник, да и сделать алгоритм проще и понятнее:
// dst - массив для сохранения вершин результата
// src - массив вершин исходного полигона
// n - число вершин исходного полигона
// функция возвращает число вершин результата
int clipLeft(vertex *dst, vertex *src, int n) {
int i, r;
vertex p1, p2;
float k;
r = 0;
for (i = 0; i < n; i++) {
p1 = src[i];
p2 = src[(i + 1) % n];
if (p1.sx >= 0) { // если начало лежит в области
dst[r++] = p1; // добавляем начало
}
// если ребро пересекает границу
// добавляем точку пересечения
if (((p1.sx > 0) && (p2.sx < 0)) ||
((p2.sx >= 0) && (p1.sx < 0)))
{
k = -p1.sx / (p2.sx - p1.sx);
dst[r].sx = 0;
dst[r].sy = p1.sy + k * (p2.sy - p1.sy);
dst[r].u = p1.u + k * (p2.u - p1.u);
dst[r].v = p1.v + k * (p2.v - p1.v);
r++;
}
}
return r;
}
Написав аналогичные куски кода для остальных трех сторон экрана, получим функцию отсечения в экран по алгоритму Сазерленда-Ходжмана.
В пунктах 3.6.1 и 3.6.2 делался упор на 2D-отсечение, т.е. отсечение экраном уже спроецированного полигона. Еще один метод - это 3D-отсечение, когда все полигоны отсекаются областью зрения камеры. В этом случае после проецирования полигон заведомо попадает в экран и дальнейшее отсечение уже не требуется. Кстати, z-отсечение при 3D-отсечение делается почти автоматически, очень хорошо вписываясь в общую схему, при использовании же 2D-отсечения придется делать еще и его. Рассмотрим стандартную камеру. Ее область зрения задается "пирамидой", ограниченной пятью плоскостями со следующими уравнениями (откуда взялось smallvalue и что это такое, написано в п.3.5):
z = -dist + smallvalue Вот рисунок (вид сбоку), на котором видно первые три из этих плоскостей. 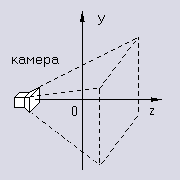 Отсекаем полигон каждой из этих плоскостей по тому же самому алгоритму Сазерленда-Ходжмана, получаем 3D-отсечение. Теперь выясним, как это самое отсечение сделать относительно универсально (а не только для стандартной камеры), быстро и просто. Зададим наши пять плоскостей не в форме какого-то уравнения, а в форме plane = [o, n], где o - какая-то точка, принадлежащая плоскости; n - нормаль, смотрящая в то полупространство, которое мы хотим оставить. Например, для стандартной камеры в этом случае плоскости запишутся так:
При такой форме задания плоскости критерий принадлежности произвольной точки p нужному нам полупространству выглядит очень просто: (p - o) * n >= 0. Не менее просто выглядит и процедура поиска пересечения отрезка от точки p1 до точки p2 с плоскостью. Для любой точки p внутри отрезка имеем p = p1 + k * (p2 - p1), 0 <= k <= 1, но так как p лежит в плоскости, p * n = 0; отсюда имеем (p1 * n) + (k * (p2 - p1) * n) = 0, и моментально находим точку пересечения. Все 3D-отсечение, таким образом, сводится к последовательному применению одной универсальной процедуры отсечения плоскостью. Кроме того, видно, что можно посчитать матрицу перевода стандартной камеры в произвольную, применить ее к выписанным точкам o и нормалям n для плоскостей, задающих "стандартную" область зрения (к нормалям, естественно, надо применить только "поворотную" часть матрицы) и получить, таким образом, уравнения плоскостей уже для *любой* камеры. Тогда 3D-отсечение можно сделать вообще до всяческих преобразований сцены, минимизировав, таким образом, количество поворотов и проецирований вершин - не попавшие в область зрения вершины поворачивать и проецировать, очевидно, не надо. Проецирования невидимых вершин, впрочем, можно избежать и другим образом: сделав поворот сцены, а потом 3D-отсечение "стандартной" областью зрения камеры. Рассмотрим это более подробно. Пусть у нас есть какая-то камера; пусть есть матрица, которая переводит стандартную камеру в эту камеру. Она как бы состоит из двух частей: матрицы T (обозначения здесь использутся те же самые, что в п.2.5) и матрицы параллельного переноса, совмещающей Ss и s (обозначим ее буквой M). Причем сначала применяется матрица M, потом матрица T. Так вот, для перевода какой-то плоскости-ограничителя области зрения стандартной камеры, заданной в форме plane = [o,n], надо всего лишь сделать пару матричных умножений (поскольку M - матрица переноса, и ее применение на деле сводится к трем сложениям, матричных умножений будет ровно два): new_o = T * M * std_o Что лучше и быстрее, как обычно, не ясно. При отсечении до преобразований тест на попадание точки в область зрения стоит от 3 до 15 умножений (относительно дешевые операции типа сложений не считаем), плюс 11 умножений и 2 деления на поворот и проецирование после отсечения, зато поворачиваются и проецируются только видимые точки. При отсечении после преобразований тест стоит 8 умножений (так как в координатах нормалей шесть нулей и одна единица), зато для всех точек придется сделать 9 умножений для поворота; проецироваться же по-прежнему будут только видимые точки. Так что наиболее подходящий метод выбирайте сами. В завершение осталось только привести процедуру для отсечения полигона произвольной плоскостью:
// вычитание векторов
float vecsub(vertex *result, vertex a, vertex b) {
result->x = a.x - b.x;
result->y = a.y - b.y;
result->z = a.z - b.z;
}
// скалярное умножение векторов
float vecmul(vertex a, vertex b) {
return a.x * b.x + a.y * b.y + a.z * c.z;
}
// dst - массив для сохранения вершин результата
// src - массив вершин исходного полигона
// num - число вершин исходного полигона
// n - нормаль к плоскости
// o - точка, лежащая в плоскости
// функция возвращает число вершин результата
int clipPlane(vertex *dst, vertex *src, int num,
vertex n, vertex o)
{
int i, r;
vertex p1, p2, tmp;
float t1, t2;
float k;
r = 0;
for (i = 0; i < num; i++) {
p1 = src[i];
p2 = src[(i + 1) % num];
vecsub(&tmp, p1, o); t1 = vecmul(tmp, n);
vecsub(&tmp, p2, o); t2 = vecmul(tmp, n);
if (t1 >= 0) { // если начало лежит в области
dst[r++] = p1; // добавляем начало
}
// если ребро пересекает границу
// добавляем точку пересечения
if (((t1 > 0) && (t2 < 0)) ||
((t2 >= 0) && (t1 < 0)))
{
k = 1 - vecmul(p1, n) / vecmul(p2, n);
dst[r].x = p1.x + k * (p2.x - p1.x);
dst[r].y = p1.y + k * (p2.y - p1.y);
dst[r].z = p1.z + k * (p2.z - p1.z);
dst[r].u = p1.u + k * (p2.u - p1.u);
dst[r].v = p1.v + k * (p2.v - p1.v);
r++;
}
}
return r;
}
|
 |
|
