Если Вы найдете статью полезной и интересной - не сочтите за труд,
переведите материал или хотя бы часть его и отправьте на адрес
algolist@manual.ru.
Задать вопросы или просто написать письмо можно
также на странице контактов.
Viktor T. Toth
web: http://www.vttoth.com/
No wonder mathematicians find numbers to be the passion of a lifetime.
Deceptively simple things can lead to such amazing complexity, to intriguing
links between seemingly unconnected concepts.
Take the simple concept of the factorial. The factorial of a positive
integer, n, is defined as the product of all the integers between 1 and
n inclusive. Thus, for instance, the factorial of 5 is 5!=1×2×3×4×5, or
120. Because n!=n×(n-1)!, and conversely,
(n-1)!=n!/n, it is possible to define 0! as 1!/1, or
1.
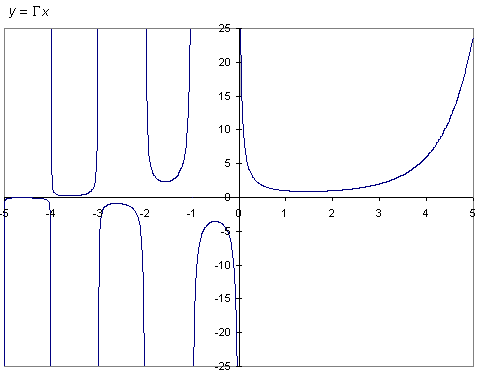
If you plot the factorial of integers on a graph, you'll notice that the
points you plotted will be along what appears to be some kind of an exponential
curve. In any case, it looks very much possible to connect the points with a
smooth line. This begs the question: might it be possible to extend the
definition of the factorial and create a smooth function that has a value for
all real numbers, not just integers, but for integers, its value is equal to
that of the factorial itself?
The answer is a resounding yes; such a function indeed exists. In fact, the
so-called Gamma function extends the definition of the factorial to the entire
complex plane. In other words, while the factorial is defined only for
non-negative integers, the Gamma function is defined for any complex number
z as long as z is not a negative integer.
Definition
The Gamma function is defined by the following integral:
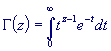
For all complex numbers z, the following recurrence relation is
true:
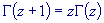
Consequently, for positive integers:

Some very helpful relationships exist between the Gamma function values for
various arguments. For instance, the following relationship makes it possible to
compute the Gamma function for a negative argument easily:
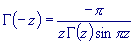
But how do you actually compute the Gamma function? The definition
integral is not very useful; to produce an accurate result, an insanely high
number of terms would have to be added during some numerical integration
procedure. There must be some other way; there indeed is another way, several
other ways in fact, each yielding useful algorithms for handheld
calculators.
The Numerical Recipes Solution
Back in 1979, when I was possessed with the desire to squeeze a Gamma
function implementation into the 72 programming steps of my tiny calculator, I could not find any
ready reference on numerical approximations of this function. Eventually, I came
across a 1955 Hungarian book on differential and integral calculus, which
provided a usable approximation formula. Being theoretical in nature, the book
offered not only no hints on efficient computation of the function, it didn't
even provide numerical approximations of the coefficients in the formula; that
was all left to the reader to work out (or to not work out, as might be the
case, since theoretical mathematicians rarely sink to the level of actually
working out a numeric result). Work it out I did, making my little calculator
run for several days from its wall charger, while it calculated some of
those coefficients. Eventually I had my result: a 71-step program that provided
8 or more digits of precision for real z's in the range of 0.5 <
z < 1.5. From these values, it is possible to compute the Gamma
function of any real number using the recurrence relation.
As it turns out, while my approximation is not a bad one, there's a much
better method for calculating the Gamma function. Numerical Recipes in
C (2nd ed. Cambridge University Press, 1992) demonstrates a much more
efficient algorithm, the so-called Lanczos approximation for computing
the Gamma function for any positive argument (indeed, for any complex
argument with a nonnegative real part) to a high level of accuracy. Here is
their magic formula, computing the Gamma function with an error that's smaller
than 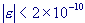 for any complex z for which Re z
> 0: for any complex z for which Re z
> 0:
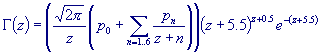
where
p0 =
1.000000000190015
p1 =
76.18009172947146
p2 =
-86.50532032941677
p3 =
24.01409824083091
p4 =
-1.231739572450155
p5 =
1.208650973866179 ·
10-3
p6 =
-5.395239384953 · 10-6
Примечание: более получить более общую формулу наряду с некоторой интересной информацией и исходниками можно в оригинальной статье Numerical Recipeszip
The calculation can be simplified resulting the following formula:
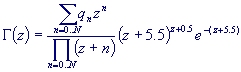
| q0 = |
75122.6331530 |
| q1 = |
80916.6278952 |
| q2 = |
36308.2951477 |
| q3 = |
8687.24529705 |
| q4 = |
1168.92649479 |
| q5 = |
83.8676043424 |
| q6 = |
2.50662827511 |
The Lanczos Approximation
Numerical Recipes neglects to mention an important fact: that the
Lanczos approximation (A Precision Approximation of the Gamma
Function J. SIAM Numer. Anal. Ser. B, Vol. 1 1964. pp. 86-96)
can be used with other choices of values. It is possible to derive simpler
versions with fewer coefficients; it is also possible to develop extremely
accurate versions. As a matter of fact, the Lanczos approximation can
be used to compute the Gamma function to arbitrary precision. I am
grateful to Paul Godfrey
for providing me with the details that are presented here.
The Lanczos approximation can, in essence, be reduced to a simple
vector inner product and then some additional elementary computations:

Where Z is an n-dimensional row vector constructed
from the function argument, z:
![Z = [ 1 1/(z+1) 1/(z+2) ... 1/(z+n-1) ]](gif/make_z.gif)
And P is an n-dimensional column vector constructed
as the product of several n×n matrices and the
n-dimensional column vector F:
P =
D·B·C·F
where
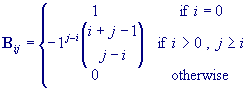
C is a matrix containing coefficients from Chebyshev
polynomials:
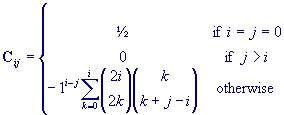
and
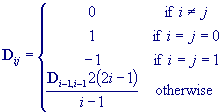
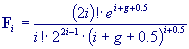
and g is an arbitrary real parameter, n is an integer. For
suitable choices of g and n, very good precision can be
obtained. The typical error can be computed as follows:
E = C·F
![|epsilon| = | [g*sqrt(pi) - Sigma(i=0,n-1) -1^i * Ei]*pi/2*sqrt(1/2e) |](gif/make_e.gif)
I endeavoured to follow up on Godfrey's work and wrote an arbitrary precision implementation
of the Lanczos approximation in the C++ language, utilizing the GMP
multi-precision library and my custom C++ wrapper classes for the functions
contained therein. This arbitrary precision implementation enabled me to
compute, for instance, the Gamma function of 101 (i.e., 100!) to full integral
precision, i.e., to a precision better than 158 significant digits.
On a more mundane level, my implementation also allowed me to experiment with
various sets of coefficients, trying to find the most accurate and economical
version of the Lanczos approximation for pocket calculators. I indeed found a
set of only 4 coefficients that has a computed precision of  <2·10-7, but in practice, appears to yield
more than 8 significant digits for all positive real arguments. The precision is
further increased when 5 or 6 coefficients are used: <2·10-7, but in practice, appears to yield
more than 8 significant digits for all positive real arguments. The precision is
further increased when 5 or 6 coefficients are used:
| n |
4 |
5 |
6 |
| g |
3.65 |
4.35 |
5.15 |
| p0 |
2.50662846436560184574 |
2.50662828350136765681 |
2.50662827563479526904 |
| p1 |
41.4174045302370911317 |
92.2070484521121938211 |
225.525584619175212544 |
| p2 |
-27.0638924937115168658 |
-83.1776370828788963029 |
-268.295973841304927459 |
| p3 |
2.23931796330266601246 |
14.8028319307817071942 |
80.9030806934622512966 |
| p4 |
N/A |
-0.220849707953311479372 |
-5.00757863970517583837 |
| p5 |
N/A |
N/A |
0.0114684895434781459556 |
 |
2·10-7 |
1·10-8 |
3·10-11 |
The simplicity of the formula for n=4 makes it suitable for use with
most programmable calculators, including some of the simplest models; and that
includes my old OEM Commodore machine. Which means the end of my quest after
more than 20 years of programming: I finally have a "perfect" method of
computing the Gamma function, to the maximum precision possible, on my first
programmable calculator.
Stirling's Formula
When great accuracy isn't required, a much simpler approximation exists for
the generalized factorial: Stirling's formula. In its original form, this is
what this formula looks like:
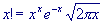
Unfortunately, this formula isn't particularly accurate. A simple
modification, however, can make it accurate to three or four significant digits
for most arguments, making it suitable for many applications:
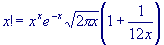
These variants may make you wonder: are there more accurate versions of
Stirling's formula? Indeed there are. Here is a generalized version for the
logarithm of the Gamma function:
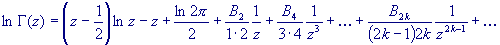
In this formula, the coefficients Bn are
derived from the so-called Bernoulli polynomials. The can easily be calculated
from the following equations (in which you'll no doubt recognize those good old
ordinary binomial coefficients):
1 + 2B1 = 0
1 +
3B1 +
3B2 = 0
1 +
4B1 +
6B2 +
4B3 = 0
1 +
5B1 +
10B2 +
10B3 +
5B4 = 0
...
And so on. The first few Bk's are:
B1=-1/2,
B2=1/6,
B3=0,
B4=-1/30,
B5=0,
B6=1/42,...
Stirling's formula is an odd bird. What you see above may suggest that the
absolute value of B's get ever smaller as the index increases, and that
therefore, Stirling's formula converges. This is not so; after
B6 in fact the absolute value of these
B's begins to increase (e.g.,
B8=-1/30) . After a while, the B's
will get very large, and subsequent sums in the approximation will swing around
ever more wildly. For instance, B98 is
approximately 1.1318×1076! Still, Stirling's formula
can be used to approximate the Gamma function quite nicely if you don't sum too
many elements of the series. In fact, the higher the real part of z is,
the more accurate the formula becomes... so one trick for the case of a small
Re z is to evaluate Stirling's formula for z+n, and
then divide the result by
z(z+1)(z+2)...(z+n-1).
One particular set of coefficients is easy to remember, procudes a relatively
compact version of Stirling's formula, and yields very good accuracy for
arguments over 5:
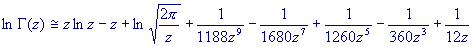
While the Lanczos approximation may be somewhat more accurate and
compact, it requires several floating point constants that may be difficult to
remember, and take up precious (program or registry) memory on your calculator.
So in many cases, using Stirling's formula may be preferable. However, it should
not be forgotten that even with corrections, it remains inaccurate for small
arguments.
The Incomplete Gamma Function
A close relative to the Gamma function is the incomplete Gamma function. Its
name is due to the fact that it is defined with the same integral expression as
the Gamma function, but the infinite integration limit is replaced by a finite
number:
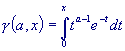
The incomplete Gamma function can be approximated fairly rapidly using an
iterative method:
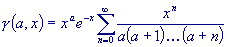
The magnitude of successive terms quickly diminishes as n increases;
8-12 digit accuracy is achieved for most values of xand a
after no more than a few hundred terms (often less than a hundred) are
added.
The incomplete Gamma function can also be used to approximate the value of
the Gamma function itself, by selecting a suitable high integration limit
x. For a<50, x=30, 8-digit accuracy is
achieved.
|