In 1985, Fortune invented an interesting algorithm for construction of Voronoi diagram. He used
the sweep-line strategy implemented by many algorithms of computer graphics and computational
geometry. The idea of the algorithm is very simple and its time complexity is O(n log2 n)
in the worst case, where n is the number of input points. In the continuation, an idea of the
algorithm is shortly given; details can be find in [BERG97].
Fortune has expanded his observation in 3D. He put coins above all points from set P.
All coins are slanted for an angle of 45°. These coins are scanned with a scanning plane
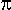 , which is also slanted for an angle of 45° to the xy
plane (Figure 2). , which is also slanted for an angle of 45° to the xy
plane (Figure 2).
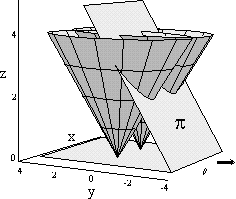
Figure 2: During the process of scanning, plane  intersects coins intersects coins
In Fortune's method, we are interested in intersections of the scanning plane with coins. These
intersections represent a curve of parabolic arcs or parabolic front. This curve has the
property that joints of parabolic arcs lie on intersection of two neighboring coins. The
parallel projection of these two coins on xy-plane represents exactly bisector on which Voronoi
edge lies. At first, the method seems very complicated, but Fortune has had the fortune on his
side. If the coins and sweep plane are considered in xy-plane, we get the sweep line and
parabolic front. In Figure 3 it is easy to see why the curve of the parabolic front is so
important. Namely, Voronoi diagram is fully constructed above the parabolic front and below we
do not know anything about it.
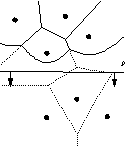
Figure 3: 2D representation of Fortune's method; Voronoi diagram is constructed only above parabolic front
From Figure 3, it can be seen that a topological structure of the parabolic front is changed by
sliding the scanning line over xy-plane. Here the major problem in the construction of data
structures is met. Namely: "When and how the topological structure of parabolic front is changing?"
The answer is hidden in events. Two kinds of events appear. The first is a point event and the
second a circle event.
|