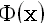 с произвольной точностью: ошибки всегда возникают из-за конечной разрядности.
Алгоритмы основаны на разложении в ряды Тейлора и цепные дроби функций,
связанных с
с произвольной точностью: ошибки всегда возникают из-за конечной разрядности.
Алгоритмы основаны на разложении в ряды Тейлора и цепные дроби функций,
связанных с 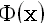 простыми соотношениями. Структура всех этих алгоритмов описывается в приложении
А; коды на Си содержатся в приложениях В и Г.
простыми соотношениями. Структура всех этих алгоритмов описывается в приложении
А; коды на Си содержатся в приложениях В и Г.
Вероятно, наиболее известными соотношениями, позволяющими вычислять
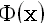 с произвольной точностью, являются
с произвольной точностью, являются
(1)= 0.5 + I(x),
.
Это разложение легко получить, интегрируя почленно разложение Тейлора
в нуле функции exp(-x2/2).
Хотя при этом получается знакопеременный ряд, первый отброшенный его член
не является, вообще говоря, верхней границей для остатка, т.к. его члены
монотонно убывают, лишь начиная с некоторого. Тем не менее, довольно легко
убедиться в том, что при
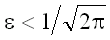 =0.3989...
это приятное свойство имеет место. А так как в любой практической задаче
=0.3989...
это приятное свойство имеет место. А так как в любой практической задаче
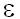 <<0.1,
можно считать, что если выполнено неравенство
<<0.1,
можно считать, что если выполнено неравенство
(2) 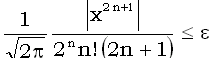 ,
,
то сумма n
первых членов ряда доставляет
I(x)
с точностью 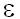 (если, конечно, не учитывать накопление ошибки).
(если, конечно, не учитывать накопление ошибки).
Алгоритм I. Этот алгоритм основывается на разложении (1). Обратите внимание: при n-м выполнении шага I2 переменная m равна 2n, так что t здесь делится все-таки на 2nn!. Разложение (1) было использовано в алгоритме 272 [12], который, однако, значительно менее экономен, чем нижеследующая версия.
 , где
, где  .
.
Это разложение для ![]() можно
получить почленным интегрированием ряда Тейлора функции j(x)/j(t)
в нуле. Для остатка
можно
получить почленным интегрированием ряда Тейлора функции j(x)/j(t)
в нуле. Для остатка ![]() ряда
(3) справедливы оценки
ряда
(3) справедливы оценки
(4) ![]() .
.
Неравенства (2) и (4) показывают, что скорость сходимости разложений (1) и (3) падает с ростом x.
Алгоритм T. Этот алгоритм основан на разложении (3). В работах [1, 11] в аналогичном алгоритме на шаге T1 производится присвоение t = sum = |x|*exp(-x2/2)/Ц2pс очевидным изменением шага T4. Так как, однако, шаг T3 там не изменен, условием останова оказывается |sn+1 - sn| < e*exp(x2/2)/Ц2p, что, согласно (4), не гарантирует необходимую точность вычисления F(x). Тем не менее, если вычисление F(x)производится с машинной точностью (и машинный нуль достаточно мал) и ошибка при вычислении экспоненты не слишком велика, алгоритмы в [1, 11] дают в пределах представления чисел с плавающей запятой правильный результат.
(5) 
Эту цепную дробь можно получить разными способами (см., например, [2,3]).
Члены ее звеньев альтернируют и потому характер сходимости ее подходящих
дробей довольно сложен. Однако, для подпоследовательности подходящих дробей
с четными номерами можно показать, что ее четные члены сходятся к ![]() монотонно
возрастая, а нечетные – монотонно убывая. Поэтому модуль разности |w2n-2-w2n|
двух соседних подходящих дробей этой подпоследовательности оценивает сверху
уклонение каждой из них от
монотонно
возрастая, а нечетные – монотонно убывая. Поэтому модуль разности |w2n-2-w2n|
двух соседних подходящих дробей этой подпоследовательности оценивает сверху
уклонение каждой из них от ![]() .
.
Алгоритм S. В данном алгоритме, основанном на разложении (5), для получения подпоследовательности подходящих дробей с четными номерами мы производим на каждом витке цикла вычисление двух очередных подходящих дробей; соответствующее рекурсивное соотношение для сжатой дроби слишком сложно и потому не использовано.
(6') wn-1-wn = (-1)n(4n-1)(2n-2)! x4n-1/(q2n-2q2n),
(6") 
показывают, что необходимое число подходящих дробей растет с ростом x. Поэтому разложение следует применять лишь при небольших значениях x; сам Л.Шентон [13] рекомендует применять его только при x <Ц3.
До сих пор мы имели дело с разложениями, "качество" которых ухудшалось с ростом x. Рассмотрим теперь соотношения, которые с ростом x позволяют вычислять F(x) все быстрее:
(7') F(x) = 0.5 + j(x)R(x),
(7") 
Функция R(x) называется отношением Миллса. Разложение в цепную дробь для него было предложено еще Лапласом в 1805 г. Члены звеньев этой цепной дроби при x > 0 положительны и потому (см., например, [6]) подходящие дроби с четными номерами сходятся к R(x) монотонно возрастая, а с нечетными – монотонно убывая. Поэтому модуль разности
двух соседних подходящих дробей этой подпоследовательности оценивает сверху уклонение каждой из них от R(x). Можно показать, что имеет место оценка
(8)  ,
,
из которой следует, что скорость сходимости разложения растет с ростом x.
Алгоритм L. В этом алгоритме F(x)вычисляется с помощью разложения отношения Миллса R(x) в цепную дробь Лапласа (7).
(9)  ,
,
который легко получить, проинтегрировав отношение Миллса R(x)
по частям. По заданному e
можно найти xe,
такой, что при x
і
xe, ряд (9) позволяет
вычислять F(x)
с точностью e. Однако,
с помощью этого ряда невозможно, вообще говоря, достичь в любой заданной
точке x произвольной
точности, поэтому мы и не исследуем алгоритм, основанный на этом разложении.
Для проведения численных экспериментов алгоритмы I, T,
S
и L были реализованы на Си. В нижеследующей таблице для каждого
алгоритма в столбце N
приводится количество "витков" цикла, потребовавшихся для вычисления значения
с e = 0 для нескольких
x;
поскольку все алгоритмы дали одинаковые 8 знаков после запятой, сами вычисленные
значения опущены. В столбце O приводится число потребовавшихся операций.
Для алгоритма I оно вычислялось по формуле
8+11ґN,
для алгоритма T – по формуле 14+8ґN,
для S – по формуле 23+25ґN,
наконец, для L – по формуле 16+10ґN.
Обратите внимание – всем операциям, в том числе, таким, как вызов функции
fabs
или exp, придается равный вес. Для иллюстративных целей такая
точность признана достаточной.
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим графики, отражающие данные из этой таблицы, – их проще анализировать.
На нижеследующих рисунках слева – столбцы N,
справа – O.

а) число витков цикла |

б) количество операций |
Мы видим, что по числу N витков цикла алгоритмы при не слишком больших x практически не различаются до x»3.5, после чего лидирует алгоритм S. Начиная с x» 4, бесспорным лидером становится алгоритм L. По числу операций, конечно, более важной характеристике, до x» 4 лидером является алгоритм T, после – снова алгоритм L.
Помимо превосходства в скорости алгоритм T выгодно отличается от I и S устойчивостью по отношению к накоплению ошибки. Для доказательства высказанного утверждения оценим распространяемую ошибку округления.
Пусть ![]() –
относительная ошибка n-й
частичной суммы в алгоритме I, а
–
относительная ошибка n-й
частичной суммы в алгоритме I, а ![]() –
относительная ошибка tn.
Для простоты предполагаем, что представление целых чисел и действия над
ними осуществляются без ошибок, а ошибки округления всех арифметических
операций над действительными числами не превосходят r.
Тогда для
–
относительная ошибка tn.
Для простоты предполагаем, что представление целых чисел и действия над
ними осуществляются без ошибок, а ошибки округления всех арифметических
операций над действительными числами не превосходят r.
Тогда для ![]() имеем
следующее соотношение
имеем
следующее соотношение
(10)  ,
,
причем
(11) ![]()
где ![]() –
относительная ошибка представления x2.
Будем считать также, что
–
относительная ошибка представления x2.
Будем считать также, что
(12) ![]() .
.
Верхняя оценка ошибки (12) растет с пугающей скоростью: так, если r=10-10,
то ![]() , а
, а ![]() .
При этом следует учесть, что при выводе мы игнорировали знакопеременность
ряда (1), а это сильно смягчает грубость оценки (12).
.
При этом следует учесть, что при выводе мы игнорировали знакопеременность
ряда (1), а это сильно смягчает грубость оценки (12).
Для алгоритма T относительная ошибка ![]() частичной
суммы sn
также удовлетворяет соотношению (10), однако теперь
частичной
суммы sn
также удовлетворяет соотношению (10), однако теперь ![]() .
Действуя, как раньше, получаем оценку
.
Действуя, как раньше, получаем оценку
(13) ![]() .
.
Эта оценка возрастает лишь немного медленнее, чем оценка (12), Однако, члены ряда (6) положительны, поэтому истинная относительная ошибка значительно меньше полученной оценки (13). Хотя общий член ряда (2) убывает быстрее, чем общий член ряда (3), машинные эксперименты показывают, что число исполнений шага T2 меньше числа «витков цикла» в алгоритме I; это также приводит к меньшей распространяемой ошибке. Тем не менее, на точность вычисления F(x) сильно влияет точность вычисления exp(-x2/2): возникающая здесь ошибка может «съесть» все преимущества разложения (3).
Полученные данные позволяют рекомендовать для вычисления F(x) с произвольной точностью сочетание алгоритмов T и L. Нужно только выбрать точку p, разделяющую области действия этих алгоритмов.
Итак, при возрастающих x время счета по алгоритму T возрастает, а по алгоритму L убывает. Поэтому в качестве p следовало бы выбирать точку, в которой эти времена становятся равными. К сожалению такая точка зависит от точности счета e , от разрядности используемого компьютера, от его скорости. Поэтому выбрать навеки оптимальную» точку p не удастся; я рекомендую выбирать ее при e , равном машинному нулю.