Да-да, это именно тот метод, с помощью которого смазывают текстуры всякие ускорители типа 3Dfx. Итак, пусть у нас есть какая-то текстура. Текстура у нас - это 2D картинка, а 2D картинка в свою очередь - набор замеров цвета через какие-то промежутки. В реальной же жизни цвет не меняется скачком через каждый, например, миллиметр, а является какой-то непрерывной функцией от положения, причем меняется довольно плавно. При обычном текстурировании мы получаем координаты в текстуре, округляем их до ближайшего целого числа и выбираем нужный цвет из текстуры. То есть мы как бы берем значение цвета в самой близкой к рисуемой точке сетки замеров цвета, поэтому у нас цвет резко меняется, оставаясь непрерывным между узлами сетки, поэтому возникает эффект больших квадратов. При билинейной фильтрации цвет всего-навсего линейно интерполируется между узлами сетки замеров. То есть. Пусть в текущей точке у нас получились координаты текстуры u, v - какие-то нецелые, вообще говоря, числа. Тогда по целым частям u, v определяется, между какими узлами сетки (если угодно, между какими пикселами текстуры) находится наша точка, а по дробным - как близко она находится к каждому из узлов. Вот картинка. 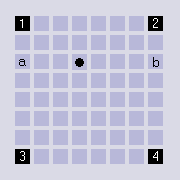 Здесь 1, 2, 3, 4 - "окружающие" точку пикселы текстуры (они же узлы сетки замера цвета). Пусть iu, iv - целые части координат текстуры точки u, v; fu, fv - дробные части. Тогда 1, 2, 3, 4 имеют координаты в текстуре (iu,iv), (iu+1,iv), (iu,iv+1), (iu+1,iv+1). Проинтерполируем какую-то компоненту цвета (R, G или B) по прямым 1-3 и 2-4: a.c = 1.c + (3.c - 1.c) * fv, то есть a.c = c[iu][iv] + (c[iu][iv+1] - c[iu][iv]) * fv, Теперь проинтерполируем цвет по прямой ab в нашей точке: c = a.c + b.c * fu, Проинтерполировав по этой формуле каждую компоненту цвета, получим наконец готовый результат - цвет точки, но уже с учетом билинейной фильтрации. Здесь у нас получилось по три умножения на компоненту. То есть в сумме девять умножений на пиксел. Можно, конечно, честно считать по этим формулам, делая девять умножений для каждого пиксела. Но можно заменить все умножения на выборки по таблице. u, v обычно - это fixedpoint; fu, fv - тоже (кстати, в случае с fixedpoint целые и дробные части вычисляются ровно одним and'ом). Пусть мы используем 24-битный цвет и 16:16 fixedpoint; тогда одна компонента цвета занимает 8 бит, а дробную часть можно одним сдвигом перевести в 24:8 fixedpoint. Получаем 256 возможных значений для любой компоненты цвета и 256 возможных значений для дробной части, то есть - табличка 256x256. Если цвет 15/16-битный, или используется более грубое (скажем, до пяти бит) округление дробной части, то табличка становится еще меньше. Памяти, конечно, не жалко, но кэш-память пока не резиновая, так что чем меньше lookup-таблица, тем оно лучше для скорости. Вот и все. Осталось только упомянуть, что лучше занести в табличку не байты, а слова, для данного примера это будет 8:8 fixedpoint, и складывать все результаты тоже как слова, а потом сдвигом переводить обратно в целые числа. Иначе (особенно в случае 15/16-битных режимов) будет заметен небольшой шум на текстуре, появляющийся из-за ошибок округления. |
 |
|
