Алгоритм быстрой сортировки
QuickSort – это классический алгоритм декомпозиции. Чтобы отсортировать массив, выбирается расщепляющий элемент и производится разбиение: элементы переставляются так, чтобы меньшие элементы оказались по одну сторону, а большие по другую, а затем полученные два подмассива рекурсивно сортируются. Что происходит с элементами, равными расщепляющему значению? В методе Хоара меньшие элементы отправляются влево, а большие вправо, равные элементы могут оказаться в любой из двух сторон.Разработчики алгоритмов давно осознали преимущества и трудности троичного разбиения. Седжвик
[22] на странице 244 замечает: «В идеале, мы хотели бы разместить все равные ключи в файле так, чтобы все ключи с меньшим значением оказались слева, а с большим – справа. К сожалению, до сих пор не изобретен эффективный способ сделать это...» Дейкстра излагает эту проблему, как «Задачу о Датском национальном флаге»: требуется упорядочить последовательность красных, белых и голубых камешков так, чтобы они следовали в порядке цветов на знамени Голландии. Это соответствует разбиению в алгоритме быстрой сортировки, когда меньшие элементы окрашиваются в красный цвет, равные в белый, а большие в голубой. Троичному алгоритму Дейкстры требуется линейное время (каждый элемент рассматривается ровно один раз), однако в оценке времени работы реализующего его кода появляется гораздо больший множитель, чем для кода, реализующего быструю сортировку Хоара.Вегнер
[27] описывает более эффективные троичные схемы разбиения. Бентли и Макклоу [2] предложили троичное разбиение, основанное на следующем инварианте цикла:
Основной цикл разбиений содержит два внутренних цикла. Первый внутренний цикл увеличивает индекс
b: он пропускает меньшие элементы, перемещает равные элементы к a, и останавливается, когда встречает больший элемент. Второй цикл, соответственно, уменьшает индекс c: он пропускает большие элементы, перемещает равные к d, и останавливается, когда встречает меньший элемент. Основной цикл затем меняет местами элементы, на которые указывают b и c, увеличивает b и уменьшает c; он останавливается, когда b и c совпадают. (Вегнер предложил тот же инвариант, однако, его коды сложнее). Работа завершается тем, что равные элементы перемещаются из концов в середину массива, при этом уже не нужны сравнения. Для разбиения n-элементного массива этому алгоритму требуется n-1 сравнение.Алгоритм внутренней сортировки анализировали разные авторы, в том числе Хоар
[9], ван Эмдер [26], Кнут [11] и Седжвик [23]. В формулировке точных результатов используются гармонические числа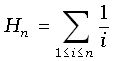 .
.
Теорема 1
[Хоар]. Алгоритм быстрой сортировки с расщепляющими элементами, выбираемыми случайно, сортирует n объектов, среди которых нет равных, в среднем за 2nHn + O(n) » 1.386n lg n сравнений.В стандартных вариантах алгоритма быстрой сортировки расщепляющим элементом служит медиана случайной выборки.
Теорема 2
[Ван Эмден]. Быстрая сортировка с расщеплением вокруг медианы 2t+1 случайно выбранных элементов, сортирует n разных объектов в среднем за 2nHn/(H2t + 2 - Ht + 1) + O(n) сравнений.Увеличивая
t, мы можем приблизить среднее число сравнений к n ln n + O(n).Приведенные выше теоремы имели дело только с средними характеристиками. Чтобы гарантировать разумное время в худших случаях, мы проводим расщепление вокруг истинной медианы, которую можно вычислить за
cn сравнений. (В работе Шенхаге, Патерсона и Пиппендера [20] рассмотрен алгоритм для худшего случая, в котором c = 3; Флойд и Риверст [8] рассматривают алгоритм для среднего времени, у которого c = 3/2.)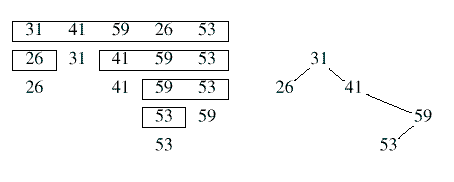
Рис. 1. Быстрая сортировка и бинарное поисковое дерево
Теорема 3. Быстрая сортировка, расщепляющая вокруг медианы, поиск которой требует cn сравнений, сортирует n элементов за cn ln n + O(n) сравнений.
Доказательство
основано на том, что в рекурсивном дереве около ln n уровней, и на каждом делается не более cn сравнений.Алгоритм быстрой сортировки тесно связан со структурой бинарных деревьев поиска (о структурах данных смотрите у Кнута
[11]). На рисунке 1 показано, как они оба обрабатывают последовательность «31 41 59 26 53». Дерево справа – это стандартное бинарное дерево поиска, сформированное вставкой элементов в порядке ввода. Рекурсивное дерево слева показывает «идеальное разбиение» быстрой сортировки: она проводит разбиение вокруг первого элемента подмассива и оставляет элементы в обоих подмассивах в том же относительном порядке. На первом уровне алгоритм проводит расщепление вокруг значения 31, и выдает левый подмассив «26» и правый подмассив «41 59 53», затем оба рекурсивно сортируются.Рисунок 1 иллюстрирует фундаментальный факт – изоморфизм между быстрой сортировкой и бинарными деревьями поиска. Необведенные расщепляющие значения слева в точности соответствуют внутренним узлам справа, как в горизонтальном, так и в вертикальном направлениях. Длина внутреннего пути дерева поиска равна общему числу сравнений, сделанных обеими структурами. Совпадают не только количества, обе структуры производят один и тот же набор сравнений. Ожидаемая стоимость успешного поиска, по определению, равна длине внутреннего пути, деленной на
n. Объединив это наблюдение с теоремой 1, получаем:Теорема 4
[Хиббард]. Среднее количество сравнений, необходимых для успешного поиска в бинарном дереве поиска, построенном вставкой элементов в случайном порядке, равно 2Hn + O(1) » 1.386 lg n.Аналогичную переформулировку допускает теорема 2: мы можем сократить цену поиска, выбрав в качестве корня поддерева медиану
2t + 1 элементов в поддереве. По аналогии с теоремой 3 сбалансированное дерево сокращает время поиска примерно до lg n.